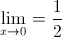Limits are an essential part of math, and will be utilized throughout our future math careers in Calculus and beyond. They show the behavior of a function/graph as it approaches a distinct number. They are important because although there may be an asymptote or hole on the graph of a function, you can still see where the graph might have gone, if the asymptote or hole were not there. These limits are somewhat more difficult than the simple limits, which require direct substitution.
Definition of a limit: If
f(x) becomes arbitrarily close to a unique number
L as
x approaches
c from either side, the limit of
f(x) as
x approaches
c is
L. This is written as:
Lim f(x)=L
Tricky Limits
Thus far, we have learned 2 ways to discover limits. These include graphing and making a table. Both of these methods require a calculator.
Graphing: Set your calculator back to function mode. Graph the given function: f(x). Find the appropriate window. Trace the function and interpret the behavior on either side of given c. The y coordinates that these points seem to approach will be L.
Table: After entering your given function press 2nd, then TBLSET to change the settings. You will want to change your independent variable from AUTO to ASK. Then go to 2nd TABLE and enter a group of x values that approach c from either side, getting as close as possible. You may want to include c itself, but it is not necessary.
Example: If c=2 you may want to include the values: 1.99,1.9,2.1,2.01, etc... This way you can accurately distinguish which value L, the graph approaches from either side.
Exceptions: There are a few cases where, although you may find a limit, it does not follow the definition and L is said to "Not Exist", in these cases, you would use the notation:
lim f(x) = DNE
1. The first case where this notation is needed is when the limit approaches infinity. PLEASE NOTE: In our earlier section on Rational Functions, we used limit notation where
lim f(x)=
, but this was just used as a convenience at the time. Infinity is not a distinct number and therefore the limit cannot approach it.
2. Another case where the limit DNE is when the limit approaches different "Ls" when approaching c from the right versus the left. Although you can use notation to designate this, when you ask for the limit of the ENTIRE function, in this case, it does not exist.
Example: F(x)= |x|/x; as x approaches 0. From the left, as x gets closer to 0, the limit seems to be -1, but from the right, as x gets closer to zero, the limit seems to be 1. In the case, lim f(x)= DNE.
3. The final case in which the limit DNE is in oscillation. In certain functions, such as sin(1/x), as the graph approaches some c, the graph oscillates, first slowly, then exponentially more quickly as you get closer. The graph will continue this forever, and will always bounce more and more quickly, looking almost like a fractal as you zoom ever closer to c.
Easy Limits
Now that we've gotten the confusing stuff out of the way, lets go on to the common cases. At most numbers c within most functions f there is a simple limit that requires direct substitution. In F(x)=x^2, the limit as x approaches 2 is 4, simply because (2)^2=4. Easy enough.
Simple Properties:
1. lim b=b
2. lim x=c
3. lim x^n=c^n
There are also rules for some simple operations you can do with limits:
1. When multiplying a scalar by a limit, multiply the scalar and L.
2. When adding or subtracting 2 distinct limits with 2 different functions, add or subract their individual Ls.
3. When multiplying or dividing 2 limits, simply multiply/divide their Ls.
4. When taking the nth power of a limit, simply raise L to the nth power.
Another easy set of rules. Just remember to operate on the Ls as you would normally, and you can't go wrong.
That's limits.