First, though, it seems fitting to do a review of fractions themselves. Here's what we know:
1. A fraction is one number being divided by another number.
4. If the numerator is greater than the denominator, the number may be expressed in multiple ways: a MIXED NUMBER or an IMPROPER FRACTION (shown in respective order)
That is all quite elementary, however. We are almost more used to seeing fractions with variables, often being RATIONAL FUNCTIONS. Rational functions are defined as one polynomial over another, like this:
Where N(x) and D(x) are both polynomials. But what's new is the idea that we can have improper fractions or mixed numbers with rational functions! Or, rather, the fact that it matters! For Example:
Clearly, the numerator has a greater magnitude than the denominator, making this an improper fraction. If one were to divide using polynomial division, they would surely end up with a mixed number. In fact, getting back to the original topic, one should divide to get the improper fraction if they are doing partial fraction decomposition. Not only should they, it is absolutely necessary. Here is an example of partial fraction decomposition:
The objective of partial fraction decomposition is to get separate fractions with just one number over the factors that make up the denominator on the opposite side of the = sign. Basically, the goal is to solve for A and B. So, the first thing you would do is to multiply to a common denominator...
Simplify...
At this point, they all have a common denominator, so we may simply eliminate them.
Now what? We have a bunch of crazy things going on! But wait! Isn't there some way to make a system of equations? Isn't there something similar that we have done with this before? Like...
Because 4 isn't an imaginary number, we know that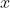 
must be equal to 
!
So, can't we do something similar to say things about the current equation we have? Yes we can!
Alright, well, there is a system of equations! Personally, I don't know how to solve the second one... I would say factor out x, but NEVER DIVIDE BY THE VARIABLE!!! And we'd still have three variables anyways... Oigh!
Anyways, for most problems that we see, we will get a number for A and a number for B and substitute them back in to the original partially decomposed fractions... Lets say HYPOTHETICALLY we solve the equations and get something. Here's what the solution should look like:
This way, it doesn't matter what variables you use or which variables are where, the solution should always be the same.
I tried to figure out what this whole crazy bit is used for, but all I can say is that is is important for calculus with integration and all kinds of great stuff that I currently have no idea exists.
That's about it for today! It's sad to think this is my last blog post... And Tom posted his before mine. It's not over, we still have more than half of a trimester ahead of us! Keep your heads up!
I hope this helps and I wish you all the best!
Shañe McPartlin
It's a nice post about . I like the way you have described it. It's really helpful. Thanks for sharing it.
ReplyDelete*It's a nice post about partial fraction decomposition
Delete