Dividing Out
If you use direct substitution in a rational function and you end up with the indeterminate form, or 0/0, then you must divide out the common factors. Once you do that, you use direct substitution in the simplified function. The only difference between the original function and simplified function is that the original had a hole at the limit value and the simplified function doesn't. But since the limit only cares about approaching the point and not the point itself, it works.
Ex.
Rationalizing Technique
Like dividing out, rationalizing is used when direct substitution results in the indeterminate form. However, if the rational function cannot be factored because of a radical, you have to rationalize it. Then, you divide out common factors and then substitute in the simplified form, just like dividing out.
Ex.
- Alexi








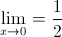
No comments:
Post a Comment